Abstract

Projection maintaining azimuths and loxodrome lengths crossing a given point – a beam of loxodromes. Mathematical foundations for projection design, pictures of graticule for world map with different positions of a given point, characteristics and specialties of projection, comparison with other projections, possibility of practical usage of projection. A projection maintaining the lengths of two loxodrome beams as one of the variants of the given projection.

Abstrakt

Zobrazení zachovávající azimuty a délky loxodrom procházejících daným bodem – svazek loxodrom. Matematické základy pro konstrukci zobrazení, obrazy zeměpisné sítě pro mapu světa při různé poloze daného bodu, vlastnosti a zvláštnosti zobrazení, porovnání s ostatními zobrazeními, možnosti praktického využití zobrazení. Zobrazení zachovávající délky dvou svazků loxodrom jako jedna z možných variant uvedeného zobrazení.

1 Úvod

Skutečnost, že kulová plocha je nerozvinutelná do roviny, je příčinou existence zkreslení na mapách. Při volbě zobrazení je možné klást na zkreslení určité (ne zcela libovolné) podmínky, které jsou potom zobrazením splněny. Jednou z možných podmínek je délkojevnost, která je u dále popsaného zobrazení aplikována na loxodromy. V případě loxodrom je v matematické kartografii nejčastěji zmiňováno Mercatorovo zobrazení, které zachovává azimuty a oblouky loxodrom zobrazuje jako úsečky, ale neumožňuje přímé měření jejich délek.

2 Vlastní zobrazení

Ze zákonitostí matematické kartografie je zřejmé, že obdobně jako není možné nalézt zobrazení zachovávající délky všech ortodrom, nelze tuto podmínku splnit ani pro všechny loxodromy. Ekvidistanci je možné požadovat pouze pro určitou soustavu čar, např. pro poledníky (zobrazení Marinovo či Ptolemaiovo) nebo rovnoběžky (ortografická projekce či Bonneovo zobrazení). Při zcela obecném vyvozování nových tříd zobrazení je možné získat zobrazení ekvidistantní ve dvou nezávislých soustavách čar – lze tedy získat zobrazení délkojevné zároveň v polednících i rovnoběžkách.

Uvedené možnosti ekvidistance v jedné i ve dvou soustavách čar byly aplikovány na loxodromy. Soustavou loxodrom je zde chápán svazek loxodrom procházejících jedním (základním) bodem, a obdobně dvěma soustavami loxodrom se chápou dva svazky procházející dvěma různými body. Zobrazení zachovávající délky jednoho svazku loxodrom je považováno za základní a je dále označováno EL1 – ekvidistantní loxodromy jdoucí jedním bodem. Zobrazení zachovávající dva svazky je analogicky označováno EL2.
 
 

3 Postup vzniku EL1

Pro možnost praktického využití délkojevnosti je nejvýhodnější, pokud se loxodromy zobrazí jako úsečky. Pak bude možno délky na mapě přímo odměřovat. Jestliže se svazek loxodrom v mapě zobrazuje jako svazek úseček se zachovanými délkami, je pro konstrukci mapy výhodné použít těchto úseček jako polárních souřadnic s počátkem v základním bodě. K délkám je potom nutné určit ještě druhou souřadnici – úhel (podmínka délkojevnosti tedy zobrazení EL1 jednoznačně nedefinuje). Jako druhá nezávislá podmínka bylo stanoveno zachování azimutů na základním bodě. Konstrukce mapy potom vychází z obou uvedených podmínek, kdy azimut A loxodromy procházející základním bodem se vypočte z rovnice

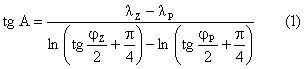
a délka l oblouku loxodromy

kde j_P, l_P jsou souřadnice koncového bodu oblouku loxodromy a R je poloměr Země. Rovnice (1) a (2) jsou zobrazovací rovnice zobrazení EL1.

Tvar zeměpisné sítě zobrazení EL1 je závislý na poloze základního bodu, resp. na jeho zeměpisné šířce. Pokud bod leží na rovníku, je obraz sítě zeměpisných souřadnic symetrický podle rovníku i základního poledníku – viz obr. 1. V případě, že základní bod neleží na rovníku, je zeměpisná síť vzhledem k rovníku asymetrická – viz obr. 2 a 3.
 
 
 
 

4 Vlastnosti a možné uplatnění zobrazení EL1

Základními vlastnostmi, na základě kterých je zobrazení zkonstruováno, je délkojevnost svazku loxodrom a zachování jejich azimutů na základním bodě. Z těchto vlastností vyplývá, že základní poledník a základní rovnoběžka jsou úsečky na sebe kolmé a délkově zachované (jedná se o dvě konkrétní loxodromy ze svazku). Z obrázků 1 až 4 je zřejmé, že obrazy ostatních rovnoběžek jsou rovnoběžné úsečky stejně od sebe vzdálené. Vzájemná vzdálenost rovnoběžek je dána délkojevností základního poledníku, jejich tvar vyplývá z převodu zobrazovacích rovnic z polárního tvaru na pravoúhlý. Vzhledem k tomu, že obecný tvar zobrazovacích rovnic v pravoúhlých souřadnicích je Y = f(j), X = g(j , l), lze zobrazení podle [2] zařadit mezi nepravá válcová. To je ostatně patrné z obr. 1.

Jedna zajímavá vlastnost zobrazení EL1 však není z obrázků zřejmá. Obrázky 1 až 3 totiž nezachycují “úplný rozsah EL1”, ale pouze základní variantu. Tedy takovou situaci, kdy je každý bod zemského povrchu zobrazen pomocí nejkratší části loxodromy. Ve skutečnosti lze z daného základního bodu Z vést libovolným dalším bodem P (l_Z ? l_P, j_Z ? j_P) nekonečně mnoho loxodrom lišících se azimutem, resp. počtem závitů (podrobně viz [3]). Při uvážení této skutečnosti se celý svět pomocí EL1 zobrazí do nekonečného pásu – viz obr 4. Pás je ohraničen rovnoběžnými přímkovými obrazy severního a jižního pólu, rovnoběžky jsou přímky s obrazy pólů rovnoběžné, poledníky se sbíhají ve dvou bodech – průsečících obrazu základního poledníku a pólů. Vzhledem k tomu, že loxodroma o obecném azimutu má nekonečný počet závitů, není mapa světa ohraničena poledníkem protilehlým k základnímu bodu, ale obraz světa se nekonečněkrát opakuje a obrazy poledníků vytvářejí stále delší a protáhlejší oblouky. Obraz loxodromy pod obecným azimutem potom dosahuje obrazu pólu v konečné (zachované) délce závislé na azimutu a protíná nekonečněkrát všechny poledníky (nekonečný počet závitů loxodromy). Je zřejmé, že úplný obraz světa zkonstruovaný pomocí EL1 nelze prakticky sestrojit.

Vzhledem k tomu, že délky loxodrom jsou zachovány pouze pro jeden svazek, nelze zobrazení použít univerzálně pro měření délek libovolných loxodrom. Zobrazení je tedy ideální pro zjišťování délek loxodrom vycházejících z jednoho bodu (obdoba Postelova zobrazení). Výhodou zobrazení však je symetrie podle poledníku základního bodu, která v případě číslování poledníků nikoli podle zeměpisné délky, ale podle rozdílu délek, umožňuje eliminovat různé zeměpisné délky základních bodů. Další výhodou je skutečnost, že každá loxodroma s obecným azimutem protíná rovník a tedy pro každou loxodromu existuje základní bod na rovníku. Poloha základního bodu je potom dána pouze zeměpisnou délkou, jejíž vliv byl již eliminován. Zobrazení je tak možné použít pro libovolnou loxodromu zadanou bodem a azimutem, pouze je nutné provést přečíslování, resp. dodatečné číslování zeměpisné sítě. Postup by byl následující: 1. základním bodem vedu přímku pod zadaným azimutem, 2. bodu, ve kterém přímka protne zadanou rovnoběžku (znám šířku zadaného bodu), přiřadím zadanou zeměpisnou délku, 3. podle této délky očísluji ostatní poledníky. Tím mám k dispozici mapu světa se zadanou délkojevnou loxodromou. Spíše než pro konstrukci map je tedy možné zobrazení, resp. zeměpisnou síť v tomto zobrazení, použít jako nomogram pro rychlé určování délek a průběhu loxodrom.

Další možné uplatnění zobrazení EL1 je využít “úplného7 obrazu světa” – obr. 4 – pro názorné objasňování průběhu loxodromy na kouli, včetně důležitých vlastností (konečná délka, nekonečný počet závitů, závislost délky na azimutu apod.).

5 Zobrazení EL2 jako jedna z variant EL1

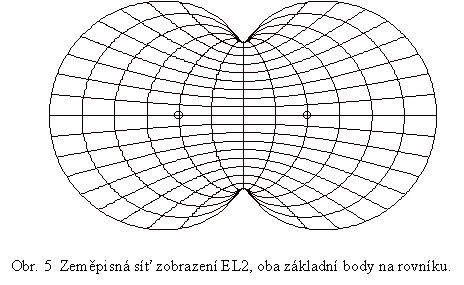
Mimo možnosti volby různé zeměpisné šířky pro základní bod lze zobrazení EL1 modifikovat pomocí druhé podmínky nutné k dourčení zobrazení (u EL1 zachování azimutů na základním bodě). Za takovou podmínku je možné zvolit požadavek délkojevnosti dvou svazků loxodrom = zobrazení EL2. Pro takové zobrazení potom budou existovat dva základní body a obrazy loxodrom budou na těchto bodech tvořit svazky úseček. Azimuty na základních bodech nebudou obecně zachovány. Jednotlivé body zemského povrchu budou potom zobrazovány jako průsečíky kružnic opsaných ze základních bodů o poloměrech rovných délkám oblouků loxodrom mezi základním a obecným bodem. Jedná se v podstatě o úlohu známou v geodézii pod označením protínání z délek. Formálně je možné převést popsaný geometrický postup na pravoúhlé nebo polární souřadnice. Tvar zeměpisné sítě získané na základě EL2 bude záviset na poloze obou základních bodů. Pro případ obou bodů na rovníku je síť zachycena na obr. 5.

6 Závěr

Účelem příspěvku bylo poukázat na některé zajímavé vlastnosti zobrazení EL1 a jeho možné modifikace. Z tohoto důvodu byl zvolen spíše geometrický popis než exaktní odvození rovnic a také nebyl proveden úplný rozbor zobrazení ve smyslu matematické kartografie, tedy analýza průběhů jednotlivých zkreslení. Představené zobrazení má některé neobvyklé vlastnosti a je možné ho využít pro speciální úlohy týkající se loxodrom.

Literatura